Bhāskara II
Bhaskara[1] (Marathi: भास्कर, Kannada: ಭಾಸ್ಕರಾಚಾರ್ಯ) (1114–1185), also known as Bhaskara II and Bhaskara Achārya ("Bhaskara the teacher"), was an Indian mathematician and an astronomer. He was born near Bijjada Bida which is in present day Bijapur district, Karnataka, India. Bhaskara was the head of an astronomical observatory at Ujjain, the leading mathematical center of ancient India. His predecessors in this post had included both the noted Indian mathematicians Brahmagupta and Varahamihira. He lived in the Sahyadri region.[1]
Bhaskara and his works represent a significant contribution to mathematical and astronomical knowledge in the 12th century. He has been called the greatest mathematician of medieval India.[2] His main work was the Siddhanta Siromani which is divided in to four parts called Lilavati , Bijaganita, Grahaganita and Goladhyaya.[3] Siddhanta Siromani is Sanskrit for "Crown of treatises".[4] The English translations of four titles are "Dealing with Arithmetic", Algebra, "Mathematics of the planets" and Sphere respectively.
Bhaskara's work on calculus predates Newton and Leibniz by half a millenium.[5][6] He is particularly known in the discovery of the principles of differential calculus and its application to astronomical problems and computations. While Newton and Leibniz have been credited with differential and integral calculus, there is strong evidence to suggest that Bhaskara was a pioneer in some of the principles of differential calculus. He was perhaps the first to conceive the differential coefficient and differential calculus.[7]
Contents |
Family
Bhaskara was born into a family belonging to the Deshastha Brahmin community.[8] History records his great-great-great-grandfather holding a hereditary post as a court scholar, as did his son and other descendants. His father Mahesvara[1] was as an astrologer, who taught him mathematics, which he later passed on to his son Loksamudra. Loksamudra's son helped to set up a school in 1207 for the study of Bhāskara's writings.[9]
Mathematics
Some of Bhaskara's contributions to mathematics include the following:
- A proof of the Pythagorean theorem by calculating the same area in two different ways and then canceling out terms to get a² + b² = c².
- Solutions of indeterminate quadratic equations (of the type ax² + b = y²).
- Integer solutions of linear and quadratic indeterminate equations (Kuttaka). The rules he gives are (in effect) the same as those given by the Renaissance European mathematicians of the 17th century
- A cyclic Chakravala method for solving indeterminate equations of the form ax² + bx + c = y. The solution to this equation was traditionally attributed to William Brouncker in 1657, though his method was more difficult than the chakravala method.
- The first general method for finding the solutions of the problem x² − ny² = 1 (so-called "Pell's equation") was given by Bhaskara II.[10]
- Solutions of Diophantine equations of the second order, such as 61x² + 1 = y². This very equation was posed as a problem in 1657 by the French mathematician Pierre de Fermat, but its solution was unknown in Europe until the time of Euler in the 18th century.
- Solved quadratic equations with more than one unknown, and found negative and irrational solutions.
- Preliminary concept of mathematical analysis.
- Preliminary concept of infinitesimal calculus, along with notable contributions towards integral calculus.
- Conceived differential calculus, after discovering the derivative and differential coefficient.
- Stated Rolle's theorem, a special case of one of the most important theorems in analysis, the mean value theorem. Traces of the general mean value theorem are also found in his works.
- Calculated the derivatives of trigonometric functions and formulae. (See Calculus section below.)
- In Siddhanta Shiromani, Bhaskara developed spherical trigonometry along with a number of other trigonometric results. (See Trigonometry section below.)
Arithmetic
Bhaskara's arithmetic text Lilavati covers the topics of definitions, arithmetical terms, interest computation, arithmetical and geometrical progressions, plane geometry, solid geometry, the shadow of the gnomon, methods to solve indeterminate equations, and combinations.
Lilavati is divided into 13 chapters and covers many branches of mathematics, arithmetic, algebra, geometry, and a little trigonometry and mensuration. More specifically the contents include:
- Definitions.
- Properties of zero (including division, and rules of operations with zero).
- Further extensive numerical work, including use of negative numbers and surds.
- Estimation of π.
- Arithmetical terms, methods of multiplication, and squaring.
- Inverse rule of three, and rules of 3, 5, 7, 9, and 11.
- Problems involving interest and interest computation.
- Arithmetical and geometrical progressions.
- Plane (geometry).
- Solid geometry.
- Permutations and combinations.
- Indeterminate equations (Kuttaka), integer solutions (first and second order). His contributions to this topic are particularly important, since the rules he gives are (in effect) the same as those given by the renaissance European mathematicians of the 17th century, yet his work was of the 12th century. Bhaskara's method of solving was an improvement of the methods found in the work of Aryabhata and subsequent mathematicians.
His work is outstanding for its systemisation, improved methods and the new topics that he has introduced. Furthermore the Lilavati contained excellent recreative problems and it is thought that Bhaskara's intention may have been that a student of 'Lilavati' should concern himself with the mechanical application of the method.
Algebra
His Bijaganita ("Algebra") was a work in twelve chapters. It was the first text to recognize that a positive number has two square roots (a positive and negative square root). His work Bijaganita is effectively a treatise on algebra and contains the following topics:
- Positive and negative numbers.
- Zero.
- The 'unknown' (includes determining unknown quantities).
- Determining unknown quantities.
- Surds (includes evaluating surds).
- Kuttaka (for solving indeterminate equations and Diophantine equations).
- Simple equations (indeterminate of second, third and fourth degree).
- Simple equations with more than one unknown.
- Indeterminate quadratic equations (of the type ax² + b = y²).
- Solutions of indeterminate equations of the second, third and fourth degree.
- Quadratic equations.
- Quadratic equations with more than one unknown.
- Operations with products of several unknowns.
Bhaskara derived a cyclic, chakravala method for solving indeterminate quadratic equations of the form ax² + bx + c = y. Bhaskara's method for finding the solutions of the problem Nx² + 1 = y² (the so-called "Pell's equation") is of considerable importance.[10]
He gave the general solutions of:
- Pell's equation using the chakravala method.
- The indeterminate quadratic equation using the chakravala method.
He also solved:
- Cubic equations.
- Quartic equations.
- Indeterminate cubic equations.
- Indeterminate quartic equations.
- Indeterminate higher-order polynomial equations.
Trigonometry
The Siddhanta Shiromani (written in 1150) demonstrates Bhaskara's knowledge of trigonometry, including the sine table and relationships between different trigonometric functions. He also discovered spherical trigonometry, along with other interesting trigonometrical results. In particular Bhaskara seemed more interested in trigonometry for its own sake than his predecessors who saw it only as a tool for calculation. Among the many interesting results given by Bhaskara, discoveries first found in his works include the now well known results for 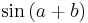 and
and 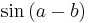 :
:
Calculus
His work, the Siddhanta Shiromani, is an astronomical treatise and contains many theories not found in earlier works. Preliminary concepts of infinitesimal calculus and mathematical analysis, along with a number of results in trigonometry, differential calculus and integral calculus that are found in the work are of particular interest.
Evidence suggests Bhaskara was acquainted with some ideas of differential calculus. It seems, however, that he did not understand the utility of his researches, and thus historians of mathematics generally neglect this achievement. Bhaskara also goes deeper into the 'differential calculus' and suggests the differential coefficient vanishes at an extremum value of the function, indicating knowledge of the concept of 'infinitesimals'.[11]
- There is evidence of an early form of Rolle's theorem in his work:
- If
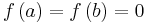 then
then 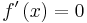 for some
for some 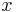 with
with 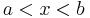
- If
- He gave the result that if
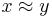 then
then 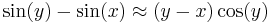 , thereby finding the derivative of sine, although he never developed the notion of derivatives.[12]
, thereby finding the derivative of sine, although he never developed the notion of derivatives.[12]
- Bhaskara uses this result to work out the position angle of the ecliptic, a quantity required for accurately predicting the time of an eclipse.
- In computing the instantaneous motion of a planet, the time interval between successive positions of the planets was no greater than a truti, or a 1⁄33750 of a second, and his measure of velocity was expressed in this infinitesimal unit of time.
- He was aware that when a variable attains the maximum value, its differential vanishes.
- He also showed that when a planet is at its farthest from the earth, or at its closest, the equation of the centre (measure of how far a planet is from the position in which it is predicted to be, by assuming it is to move uniformly) vanishes. He therefore concluded that for some intermediate position the differential of the equation of the centre is equal to zero. In this result, there are traces of the general mean value theorem, one of the most important theorems in analysis, which today is usually derived from Rolle's theorem. The mean value theorem was later found by Parameshvara in the 15th century in the Lilavati Bhasya, a commentary on Bhaskara's Lilavati.
Madhava (1340–1425) and the Kerala School mathematicians (including Parameshvara) from the 14th century to the 16th century expanded on Bhaskara's work and further advanced the development of calculus in India.
Astronomy
Using an astronomical model developed by Brahmagupta in the 7th century, Bhaskara accurately defined many astronomical quantities, including, for example, the length of the sidereal year, the time that is required for the Earth to orbit the Sun, as 365.2588 days which is same as in Suryasiddhanta. The modern accepted measurement is 365.2563 days, a difference of just 3.5 minutes.
His mathematical astronomy text Siddhanta Shiromani is written in two parts: the first part on mathematical astronomy and the second part on the sphere.
The twelve chapters of the first part cover topics such as:
- Mean longitudes of the planets.
- True longitudes of the planets.
- The three problems of diurnal rotation.
- Syzygies.
- Lunar eclipses.
- Solar eclipses.
- Latitudes of the planets.
- Sunrise equation
- The Moon's crescent.
- Conjunctions of the planets with each other.
- Conjunctions of the planets with the fixed stars.
- The patas of the Sun and Moon.
The second part contains thirteen chapters on the sphere. It covers topics such as:
- Praise of study of the sphere.
- Nature of the sphere.
- Cosmography and geography.
- Planetary mean motion.
- Eccentric epicyclic model of the planets.
- The armillary sphere.
- Spherical trigonometry.
- Ellipse calculations.
- First visibilities of the planets.
- Calculating the lunar crescent.
- Astronomical instruments.
- The seasons.
- Problems of astronomical calculations.
Engineering
The earliest reference to a perpetual motion machine date back to 1150, when Bhāskara II described a wheel that he claimed would run forever.[13]
Bhāskara II used a measuring device known as Yasti-yantra. This device could vary from a simple stick to V-shaped staffs designed specifically for determining angles with the help of a calibrated scale.[14]
Legends
His book on arithmetic is the source of interesting legends that assert that it was written for his daughter, Lilavati. In one of these stories, which is found in a Persian translation of Lilavati, Bhaskara II studied Lilavati's horoscope and predicted that her husband would die soon after the marriage if the marriage did not take place at a particular time. To alert his daughter at the correct time, he placed a cup with a small hole at the bottom of a vessel filled with water, arranged so that the cup would sink at the beginning of the propitious hour. He put the device in a room with a warning to Lilavati to not go near it. In her curiosity though, she went to look at the device and a pearl from her nose ring accidentally dropped into it, thus upsetting it. The marriage took place at the wrong time and she was soon widowed.
Bhaskara II conceived the modern mathematical convention that when a finite number is divided by zero, the result is infinity. In his book Lilavati, he reasons: "In this quantity also which has zero as its divisor there is no change even when many [quantities] have entered into it or come out [of it], just as at the time of destruction and creation when throngs of creatures enter into and come out of [him, there is no change in] the infinite and unchanging [Vishnu]".[15]
Notes
- ↑ 1.0 1.1 1.2 Pingree 1970, p. 299.
- ↑ Chopra 1982, pp. 52–54.
- ↑ Poulose 1991, p. 79.
- ↑ Plofker 2009, p. 71.
- ↑ Seal 1915, p. 80.
- ↑ Sarkar 1918, p. 23.
- ↑ Goonatilake 1999, p. 134.
- ↑ Chopra 1982, p. 52.
- ↑ Plofker 2007, p. 447.
- ↑ 10.0 10.1 Stillwell1999, p. 74.
- ↑ Shukla 1984, pp. 95-104.
- ↑ Cooke 1997, pp. 213-215.
- ↑ White 1978, pp. 52-53.
- ↑ Selin 2008, pp. 269-273.
- ↑ Colebrooke 1817.
References
- Sarkār, Benoy Kumar (1918), Hindu achievements in exact science: a study in the history of scientific development, Longmans, Green and co., http://books.google.com/books?id=p6c5AAAAMAAJ&printsec=frontcover&source=gbs_ge_summary_r&cad=0#v=onepage&q&f=false
- Seal, Sir Brajendranath (1915), The positive sciences of the ancient Hindus, Longmans, Green and co., http://books.google.com/books?id=jw88gCyGZQMC&printsec=frontcover&source=gbs_ge_summary_r&cad=0#v=onepage&q&f=false
- Pingree, David Edwin (1970), Census of the Exact Sciences in Sanskrit, Volume 146, American Philosophical Society, ISBN 9780871691460, http://books.google.com/books?id=RQoNAAAAIAAJ&printsec=frontcover&source=gbs_ge_summary_r&cad=0#v=onepage&q&f=false
- Plofker, Kim (2009), Mathematics in India, Princeton University Press, ISBN 9780691120676, http://books.google.com/books?id=DHvThPNp9yMC&printsec=frontcover&vq=bhaskara&source=gbs_ge_summary_r&cad=0#v=onepage&q=bhaskara&f=false
- Colebrooke, Henry T. (1817), Arithmetic and mensuration of Brahmegupta and Bhaskara, http://books.google.com/books?id=wYI_AAAAcAAJ&printsec=frontcover&source=gbs_ge_summary_r&cad=0#v=onepage&q&f=false
- White (1978), "Tibet, India, and Malaya as Sources of Western Medieval Technology", Medieval religion and technology: collected essays, University of California Press, ISBN 9780520035669, http://books.google.com/books?id=quCh9tAW1jcC&printsec=frontcover&source=gbs_ge_summary_r&cad=0#v=onepage&q&f=false
- Selin, Helaine (2008), "Astronomical Instruments in India", Encyclopaedia of the History of Science, Technology, and Medicine in Non-Western Cultures (2nd edition), Springer Verlag Ny, ISBN 9781402045592
- Shukla, Kripa Shankar (1984), "Use of Calculus in Hindu Mathematics", Indian Journal of History of Science 19: 95–104
- Cooke, Roger (1997), "The Mathematics of the Hindus", The History of Mathematics: A Brief Course, Wiley-Interscience, pp. 213–215, ISBN 0471180823
- Poulose, K. G. (1991), K. G. Poulose, ed., Scientific heritage of India, mathematics, Volume 22 of Ravivarma Samskr̥ta granthāvali, Govt. Sanskrit College (Tripunithura, India)
- Chopra, Pran Nath (1982), Religions and communities of India, Vision Books, ISBN 9780856920813
- Goonatilake, Susantha (1999), Toward a global science: mining civilizational knowledge, Indiana University Press, ISBN 9780253211828, http://books.google.com/books?id=MdgnAiDFSLUC&printsec=frontcover&source=gbs_ge_summary_r&cad=0#v=onepage&q&f=false
- Selin, Helaine; D'Ambrosio, Ubiratan (2001), Mathematics across cultures: the history of non-western mathematics, Volume 2 of Science across cultures, Springer, ISBN 9781402002601, http://books.google.com/books?id=2hTyfurOH8AC&printsec=frontcover&source=gbs_ge_summary_r&cad=0#v=onepage&q&f=false
- Stillwell, John (2002), Mathematics and its history, Undergraduate texts in mathematics, Springer, ISBN 9780387953366, http://books.google.com/books?id=WNjRrqTm62QC&printsec=frontcover&source=gbs_ge_summary_r&cad=0#v=onepage&q&f=false
External links
|
|||||||||||||||||||||||||